Tom Mainiero |
|
My research interests are broad and constantly expanding, but their largest connected component is a tubular neighborhood of the intersection of geometry, quantum field theory, and quantum information.
A description of some select interests—directed toward a broad audience with some technical background—is below.
A technical summary of my past research directed toward mathematicians can be found here, and directed toward physicists here.
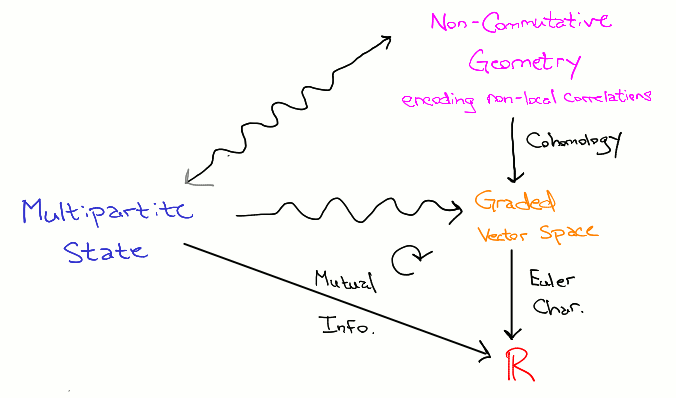
Amazingly, both classical and quantum information theory have deep connections to geometry and topology. A small hint of this connection appears when studying mutual information: a numerical quantity that measures how much information is shared between two random variables (for instance, measured in a lab by two separate "experimenters"). Mutual information is calculated as the alternating sum of entropies---another quantity is calculated this way: the Euler Characteristic of a topological space! As it so happens, this seemingly superficial observation has deep underpinnings. Understanding these underpinnings may help us derive more geometrically motivated measures of shared information, and might even be part of the puzzle of how space-time geometry can emerge from quantum entanglement (an active area of research).
Often, a firm grasp on the physics most immediately applicable to the real world is too complex to tackle directly. As a result, physicists sometimes study simpler versions of reality—"toy models"—in order to obtain a better understanding of nature. Symmetry is a great simplifier in physics and, oftentimes, such toy models typically have much greater symmetry. This symmetry is often far beyond what exists in the real world, but helps us more easily identify properties that might still exist in nature.
One such family of toy models are "field theories with extended supersymmetry" in four space-time dimensions. As the name suggests, these theories have quite a bit of symmetry, making them far easier to understand and recognize patterns within. But questions about physics in these theories also have deep connections to questions in areas of mathematics: particularly algebraic/complex geometry.
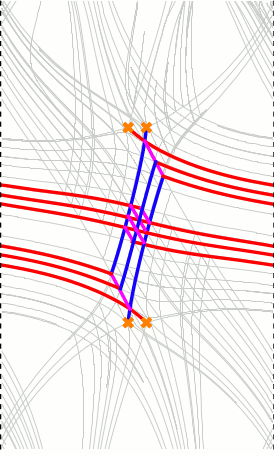
For instance one can focus on certain types of particles, called BPS particles (named after Bolgomol'nyi, Prasad, and Sommerfield) within our theory. These particles are particularly interesting as they are "stable" against small changes to physics itself. The "count" of certain types of particles in these theories turns out to be closely related to counts of geometric objects of interest to algebraic/complex geometers called "Donaldson-Thomas (DT) Invariants".
Among a myraid of other things, using ideas from physics, one can show that these "DT invariants" are actually encoded in special functions can be directly computed by studying webs or graphs that reside on a two-dimensional surface.